Bayesian theorem 을 설명하기 앞서 역확률에 대해 언급한다.
| TIP |
|
역확률 : 어떤 시행의 결과가 있을 때 그 이전 시행의 확률 구하는 과정 ex)A,B,C 세 사람이 존재하고 세사람이 가위바위보를 할때 한명이 이기는지 두명이 이기는지 비기는지 확인하는 시행 ->한 사람이 이겼을 때, 이긴 사람이 A일 확률 |
역확률의 개념을 짚어봤으니 베이스 정리(베이즈 룰)에 대해 이해해 보자.
처음 실행한 사건 A와 다음으로 시행되는 사건 B가 있다. <== 사실 이게 베이스룰과 직접 관련은 없지만 이 공식이 어디에 주로 쓰이는지 고려하면 이것이 가장 중요한 부분이니 확인하자.
여기서 우리는 조건부 확률의 정의에 의해 다음과 같은 표현을 한다.

위 수식의 의미는 조건부확률의 정의대로 A가 일어났을 때 B가 일어날 확률이다.
따라서 다음과 같은 수식도 표현이 가능하다.

수식2는 수식1의 결과를 그대로 역순이 된 조건부 확률에 적용시킨 것이다.
그리고 수식 1에서 P(AB)=P(BA)임을 고려하여 다음과 같은 식을 유도 가능한데 A,B 를 E1,E2 이벤트라 일컫게 되면 다음과 같다.

우리는 위와 같이 표현된 식을 발견자의 이름을 빌려 베이스 정리라 일컫는다.
또한 조건부 확률인 P[A|B]는 "B가 주어졌을 때 A의 Posteriori Probability "
또는 이것을 바로 "Inverse Probability(역확률)"이라고도 부른다.
여기서 더 나아가 각각의 이벤트 E1~En을 고려하면
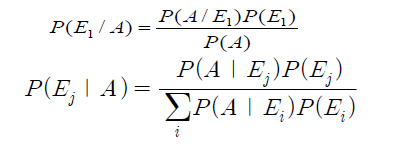
이와 같은 공식을 유도할 수 있다.
수식3에서는 전체확률의 원리 (total probability theorem)의 개념을 인지하고 있어야하니 다음 포스트에는 이것에 대해 얘기를 해보겠다.
전체확률의 원리와 베이스정리에 대해 제대로 이해를 했다면 다음 포스팅을 통해 활용을 어떻게 하는지 경험하길 바란다.
https://gkjeong.tistory.com/19?category=803575
베이스정리 적용에 사례(Example for applying the basien theorem), 후행사건이 어떻게 확률에 영향을 끼치는가?
개인적으로 정한 포스팅 스케쥴 상으로는 공학관련 포스팅과 코딩관련 글을 올려야하는데 막상 적으려고 보니 전공분야 쪽이 오히려 쉽게 설명하기가 어려워 개인적으로 아주 기초적인 부분부터 다시 공부를 하는..
gkjeong.tistory.com
'공학,과학 > 확률론' 카테고리의 다른 글
| 랜덤프로세스에 대한 대화 그리고 확률공간 (0) | 2024.02.16 |
|---|---|
| 몬티홀 문제 (12) | 2022.08.22 |
| 표본분산, 표본 표준편차에서 n-1 자유도를 이용하는 직관적인 이해. (2) | 2021.06.11 |
| 베이스정리 적용 사례(Example for applying the basien theorem), 후행사건이 어떻게 확률에 영향을 끼치는가? (0) | 2020.04.11 |
| 전체 확률의 원리 (total probability theorem), 조건부 확률 (Conditional probability) (2) | 2020.03.20 |