동적 거동을 하는 구조물의 해석에 대하여 가장 정확한 해석 방법은 시간이력해석이라는 것은 자명하게 인식된다. 그러나 해석을 진행하는데 드는 시간과, 적합한 하중을 스케일링을 진행하고 구조물에 적용하는 전 과정에 필요한 전반적인 이해력이 일반 실무자들에게 부담이 되기에 다른 여러 해석법을 주로 사용하고 있다. 대표적인 방법은 설계스펙트럼을 이용한 응답스펙트럼 해석과 지진의 동적 하중을 등가 정적하중으로 치환하는 등가정적 해석, 그리고 푸시오버 해석을 비롯한 여러 성능기반설계법 등이 있다. 건축구조기준에서 제시하는 설계 방법 중 가장 보편적인 동적해석은 응답스펙트럼 해석이다. 개인적인 생각으로는 산업이 발전할수록 건설 재료의 신뢰성이 충분히 높아지고 있고 전반적인 구조 엔지니어들의 평균 지식 수준이 높아지고 컴퓨팅 파워가 눈에 띄게 올라감에 따라 시간이력해석이 좀 더 보편화 될 가능성이 높다고 생각한다.
그럼에도 불구하고 응답스펙트럼 해석이 신뢰성과 경제성에서 충분히 유효한 보편적인 동적해석으로 인식되는데, 해당 설계법은 모드해석에 기반한다. 모드해석이란 구조물이 거동 가능한 모든 움직임을 고유치 해석을 통해 서로 관여하지 않는(모드의 직교성) 개별적 운동의 조합으로 나타내어 각 모드를 표현하는 형상벡터를 활용하여 단자유도의 구조물로 인식하는 것이다. 이를 통해 복잡한 구조물의 움직임도 여러 단자유도 움직임들의 조합을 통해 표현 할 수 있게된다. 단자유도 구조물의 경우 수계산을 진행할 수 있을 만큼 수학적으로 간단한 해석이 가능하기에(물론 그런 간단한 해석도 각각의 부재에 적용하는 힘을 계산하려면 수만개의 요소의 매트릭스 계산이 필요하고, 모드 기여율에 따라 수백가지 이상의 모드를 조합해야하는 경우도 생기므로 컴퓨터 성능이 많이 필요하다) 근대에 이루어진 이런 해석 방법의 발전은 수많은 대형 구조물의 건설에 이용되었다.
위의 내용이 무슨 얘기를 하는지 구조해석을 업으로 삼는 사람이 아니라면 알기 어려울 것이다. 심지어 해당 내용도 최대한 이해하기 쉽게 표현한 것이며 정확하게는 모드마다 단자유도에 대응하는게 아니라 모든 자유도의 움직임을 결정하는 모드 좌표계와 관련한 모드 방정식의 풀이를 진행하는 것이지만 해당 내용에 대해서는 직접 공부를해서 활용하지 않으면 글로 받아들이기 어려울 것이다.
현대에 와서는 설계프로그램들의 자동화로 근본적인 지식이 없는 기사들도 모드해석을 진행하고 있지만 해석절차의 이해 없이 해석 프로그램을 활용하는 것에는 우려가 생길 수 밖에 없다.
이번 글에서는 국내 점유율이 가장 높은 마이다스 사의 해석프로그램에서 모드해석의 결과를 직접 계산한 값을 토대로 비교를 해보려 한다. 그리고 해당 내용은 개인적인 연구 과정에서 해석프로그램의 적합성을 검증하기 위해 개인적으로 진행해본 해석 데이터 중 일부를 가져온 것이다. 마이다스 자체 내의 출력 결과에서 어떠한 값들을 활용하여 이론적으로 역산한 값과 대조하는 방법도 있지만 현재 마이다스 사에서는 공식적인 문의에도 해석 계산 과정의 중간 절차를 보여주지 않기에 그러한 것은 다루지 않을 것이며, 지금 게시 되는 자료는 매트릭스 해석과 모드해석의 기본적인 진행과정을 간략하게 다루는 것이다.
이번 글을 스스로 공부하는데 참고하거나 엔지니어 업무를 하는데 도움을 얻기 위해 사용하는 것은 가능하나 자료 자체를 활용을 하거나 출력, 펌을 하는 것에는 따로 허락을 구하길바란다.

우선 해석 프로그램상의 검토 모델과 매트랩을 통해 직접 계산한 값을 일치하는지 보기 전에 내가 해석을 진행하기 위해 머리속으로 구상한 구조물의 조건을 그대로 구성하는게 중요하다.
실제 구조물이라면 z축 회전변형을 같이 고려해야하지만 2개 질점을 가지는 4자유도 구조물을 구상했기에 건물의 구속 조건등을 그에 맞게 조정을 하였다.
그리고 각각의 자유도에 단위하중을 대입하고 1차해석을 진행하여 각 자유도에서 발생하는 변위를 확인하였다.

여기서 나타나는 변위 자체가 flexibility matrixd의 각 요소가 되며 이에 대한 역행렬을 통해 stiffness matrix를 결정할 수 있다. 이와 관련하여 공부를 하고 싶다면 'Dynamics of Structure_ Chopra' 책의 9~10장 내용을 익히면 될것이다. 개인적으로는 예제 9.5를 자주 되짚어 보곤 하였다.
이것을 통해 강성매트릭스와 질량 매트릭스를 구하게 된 후 고유치 해석을 진행하면 고유주기와 형상벡터를 구할 수 있는데 이와 과련한 내용은 이 블로그에서 면진 구조물의 해석 진행에 관해서 글을 쓸때 다룬 내용이니 참고하자.
https://gkjeong.tistory.com/79?category=823197
면진 구조물 해석에 관하여
#해당 구조물 해석을 진행할 시 계산을 간소화시키기 위하여 레일라이 감쇠를 고려한 비고전적 감쇠행렬을 고전적 감쇠행렬로 치환하여 가정하고 진행하였음을 미리 고지한다. 해당 가정은 지
gkjeong.tistory.com
해당 글에서 모드 해석에 대해 개략적인 방식은 좀 더 자세히 다뤘었기에 이 글에서는 좀 더 진행 절차에 중점을 두어 글을 진행한다.

모드별로 가지는 고유주기에 해당하는 지반가속도 값을 설계스펙트럼 가속도를 통해 구한다. 이를 통해 구해진 가속도를 모드 기여율 혹은 질량 정규화 된 상태에서의 모드 참여율을 고려해 전체 질량을 분배한 모드 유효질량에 곱하여 각각의 모드들에 작용하는 밑면 전단력을 구할 수 있다.
|
% m을 결정하고 테스트 로드를 모델에 입력한 후 테스트로드에 대한 각 질점의 변위값을
% f에 입력하면 모드별 대응 하중이 출력됨.
clear;close;clc;
m=[1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1];
% %0도
% f=[55.555556 0 55.555556 0;...
% 0 60.97561 0 60.97561;...
% 55.555556 0 69.444444 0;...
% 0 60.97561 0 76.171688]*10^-3 ;
% 30도 회전
f=[56.910569 -2.346952 56.910569 -2.346952; ...
-2.346952 59.620596 -2.346952 59.620596 ;...
56.910569 -2.346952 71.126255 -2.912982;...
-2.346952 59.620596 -2.912982 74.489877]*10^-3 ;
k=f^-1;
[Phi,omega2]=eig(k,m);
omega=omega2.^0.5;
period=2*pi()./omega;
g=9.806;
wphi_2=0;
w_phi2=0;
period=diag(period)
Sd1=0.24030;
Sds=0.42475;
Cs=[Sd1/period(1), Sd1/period(2), Sds, Sds]; %Sa/R*Ie
for n=1:4
for i=[1,3]
Phix(fix(i/2)+1,n)=Phi(i,n); % 모드형상벡터의 x성분
end
for i=[2,4] % 모드형상벡터의 y성분
Phiy(fix(i/2),n)=Phi(i,n);
end
end
for n=1:4
Mn_x(n)= ( [1,1]*Phix(:,n) )^2/ ( [1,1,1,1]*(Phi(:,n).*Phi(:,n)) ); %effective modal mass (Mn*) [1,1]은 x축 변위에 대응하는 질량 [1,1,1,1]는 전체질량
Mn_y(n)= ( [1,1]*Phiy(:,n) )^2/ ( [1,1,1,1]*(Phi(:,n).*Phi(:,n)) ); %effective modal mass (Mn*) [1,1]은 y축 변위에 대응하는 질량 [1,1,1,1]는 전체질량
end
for n=1:4
W_x(n)=Mn_x(n)*g;
V_x(n)=Cs(n) * W_x(n);
W_y(n)=Mn_y(n)*g;
V_y(n)=Cs(n) * W_y(n);
end
V_x
Vx_all=sqrt(sum(power(V_x,2)))
V_y
Vy_all=sqrt(sum(power(V_y,2)))
|
cs |

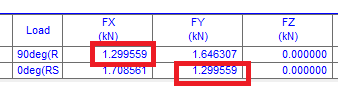
이를통해 출력값을 확인하면 다음과 같은 값이 나오며 검토 모델에서의 해당 축의 최종 밑면 전단력 값과 비교한다.
이후에 다시 질점별로 적합한 분배율을 고려하면 각 모드형상에 대응하는 하중 값들을 계산할 수 있으며, 이들을 적용한 별도의 모드들을 합성하여 전체 지진하중에 대한 해석 결과를 도출할 수 있게 된다.

|
for i=1:4
Vmsrss(i)= (V_x(i)^2 + V_y(i)^2)^0.5; % 모드별 밑면전단력 합성값
end
wi=[1,1,1,1]*g;
% Fxm1_1= (wi(1)*Phi(1,1) / sum(wi*Phi)) * Vmx(1); %mode 1의 2층바닥 x방향 하중 (wi(1)*Phi(1,1) / sum(wi*Phi)) : Cvxm 수직분포계수
% Fxm1_2= (wi(2)*Phi(2,1) / sum(wi*Phi)) * Vmx(1); %mode 1의 2층바닥 y향 하중 (wi(1)*Phi(1,1) / sum(wi*Phi)) : Cvxm 수직분포계수
for j=1:4 % j: 1~4번 모드
% for i=1:4
Cx = sum(wi(1).*Phi(1,j),'all') + sum(wi(3).*Phi(3,j),'all') ; % x 방향 Cvxm_x(수직분포계수)의 분모
Cy = sum(wi(2).*Phi(2,j),'all') + sum(wi(4).*Phi(4,j),'all') ; % y방향 Cvxm_y(수직분포계수)의 분모
% end
for i=1:4 % i: 1행: 2층바닥 x방향 하중, 2행: 2층바닥 y방향 하중, 3행: 지붕 x방향 하중, 4행: 지붕 y방향 하중
if or(i==1, i==3)
Fxm1_(i,j) = (wi(i)*Phi(i,j) / Cx) * V_x(j); % X,Y 분리 sum(wi(1).*Phi) 는 원래 모든 요소에 대해 반복해야하지만 wi의
else % 모든 요소가 같으므로 wi(1)로 wi(i)를 대체하였다.
Fxm1_(i,j) = (wi(i)*Phi(i,j) / Cy) * V_y(j);
end
end
for i=1:4 % i: 1행: 2층바닥 x방향 하중, 2행: 2층바닥 y방향 하중, 3행: 지붕 x방향 하중, 4행: 지붕 y방향 하중
Fxm2_(i,j) = (wi(i)*Phi(i,j) / Cx) * V_x(j); % x에 관하여만
end
for i=1:4 % i: 1행: 2층바닥 x방향 하중, 2행: 2층바닥 y방향 하중, 3행: 지붕 x방향 하중, 4행: 지붕 y방향 하중
Fxm3_(i,j) = (wi(i)*Phi(i,j) / Cy) * V_y(j); % y에 관하여만
end
end
fprintf('각 모드에 해당하는 하중값(각 column 마다 하나의 모드: ')
Fxm1_ %(전체 지진하중의 효과에 대응, 주축과 해석진행하는 축이 일치할때 유효)
Fxm2_ %(직교분리된 한개의 축에 대응하는 지진하중에 대응)
Fxm3_ %(직교분리된 다른 하나의 축에 대응하는 지진하중에 대응)
fyy=0; fxx=0;
for j=1:4
fy=0;
for i=[2,4]
fy=fy+Fxm2_(i,j);
end
fy=fy^2;
fyy=fyy+fy;
fx=0;
for i=[1,3]
fx=fx+Fxm3_(i,j);
end
fx=fx^2;
fxx=fxx+fx;
end
Rx_y=sqrt(fyy)
Ry_x=sqrt(fxx)
|
cs |

여기서 중요한 것은 각각의 모드에서의 하중과 변위 값은 서로 상관되지만 최종 해석된 결과에서의 하중과 변위 값은 서로 상관되지 않는다는 점이다. 이것은 동역학과 모드해석의 개념을 이해하면 자명한 결과이나 관련 지식이 없다면 상식적이지 못한 부분이다. 또 중요한 내용은 설계스펙트럼으로 사용하는 유사가속도 스펙트럼이나 혹은 유사가속도 응답스펙트럼에 대한 이해이지만 해당 내용은 별개로 다루어야할 내용이니 중요하다는 점만 짚고 넘어가겠다.
'건축,건설 관련' 카테고리의 다른 글
| 파이썬 코드_지진파 스케일링 (0) | 2021.01.21 |
|---|---|
| 지진파의 스케일링 (0) | 2021.01.21 |
| 유효좌굴길이 조정에 관해 (0) | 2020.12.15 |
| 면진 구조물 해석에 관하여 (4) | 2020.08.05 |
| 콘크리트의 내구성 계획_철근부식, 탄산화, 동해시 열화, 해안가 비말대, 부동태 등 (2) | 2020.06.12 |